中山大学海洋工程与技术学院教师在高精度无网格数值模型研究上取得进展

      光滑粒子流体动力学（SPH）是一种无网格流体力学数值模型，目前已广泛应用到船舶与海洋工程领域诸多复杂流固耦合动力学问题中。然而，传统SPH方法难以实现高阶收敛（2阶以上），这极大限制了SPH方法在复杂流动问题中的应用。

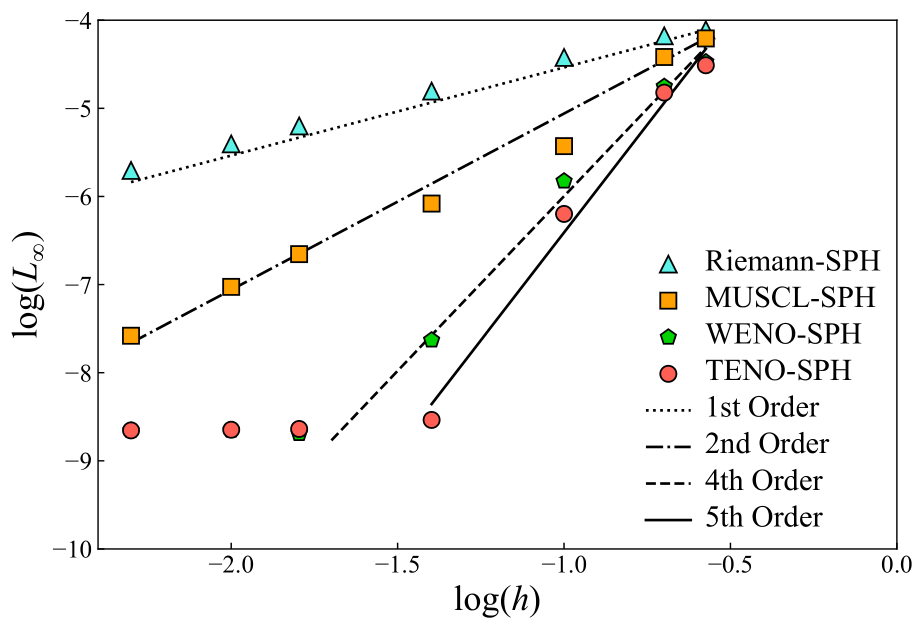
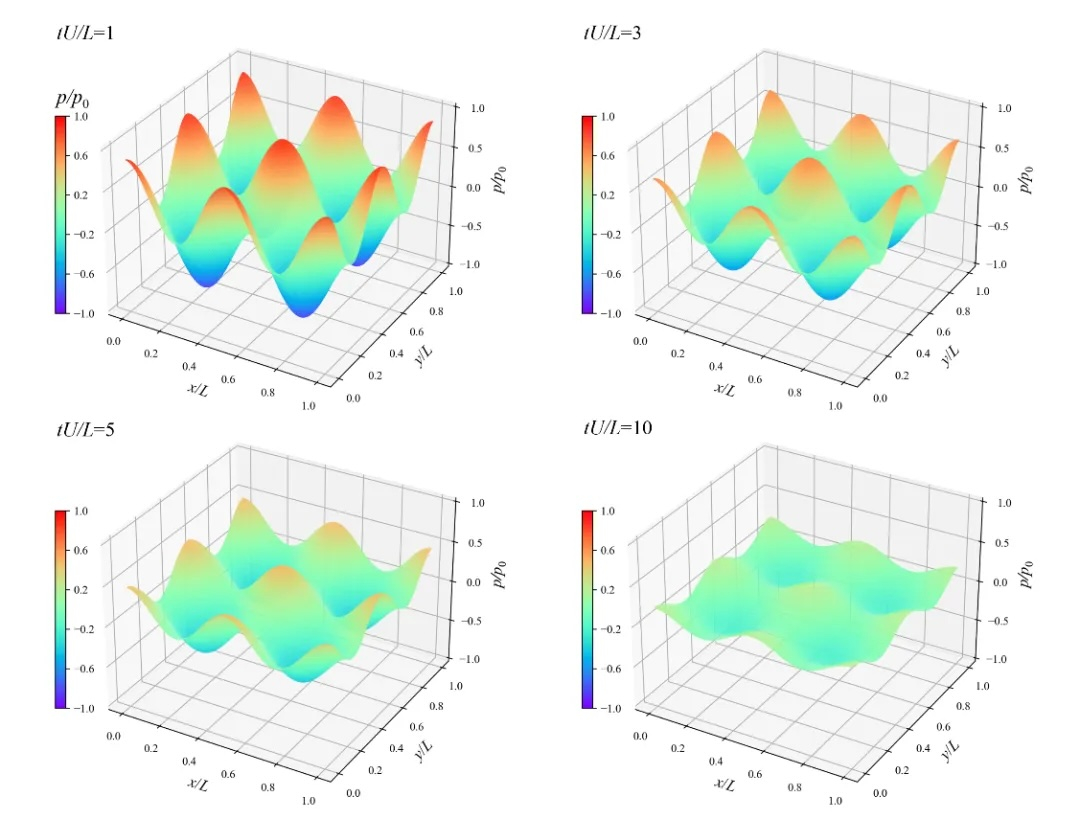
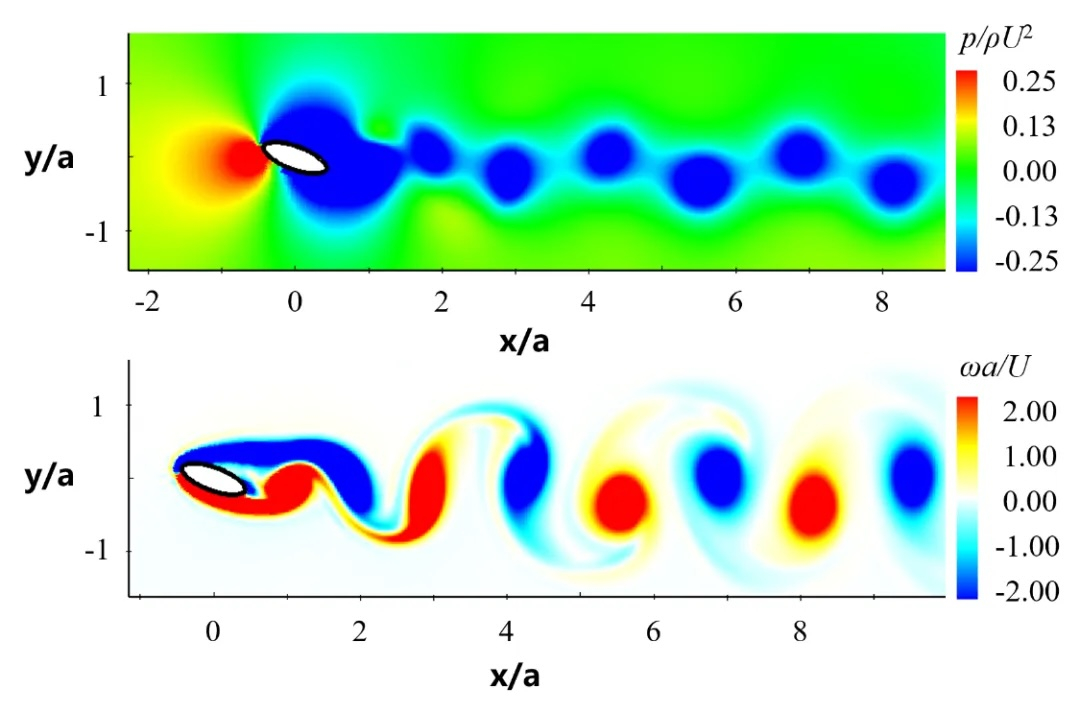
      针对该问题，中山大学海洋工程与技术学院孟子飞博士后分别建立了基于加权本质无振荡（WENO）和目标本质无振荡（TENO）重构的黎曼SPH方法，并提出了若干数值改进技术，提高计算稳定性。通过对黎曼问题中的左右状态施加W/TENO空间重构技术，降低了黎曼SPH方法的耗散，提高了SPH方法的数值精度。通过收敛性测试验证（如图1），WENO-SPH显示出4阶精度，TENO-SPH方法显示出5阶精度。经过基准算例测试，该方法在不可压粘性流动中取得了令人满意的结果，如泰勒-格林流（如图2）和椭圆柱绕流（如图3）等。

      相对于传统SPH方法，该方法以较低分辨率，获得高精度的数值模拟结果，如方腔驱动流（如图4），并在NACA0010翼型中高雷诺数绕流模拟（如图5）中得到成功应用，为后续处理复杂流动问题提供了新的无网格数值模拟方案。

 

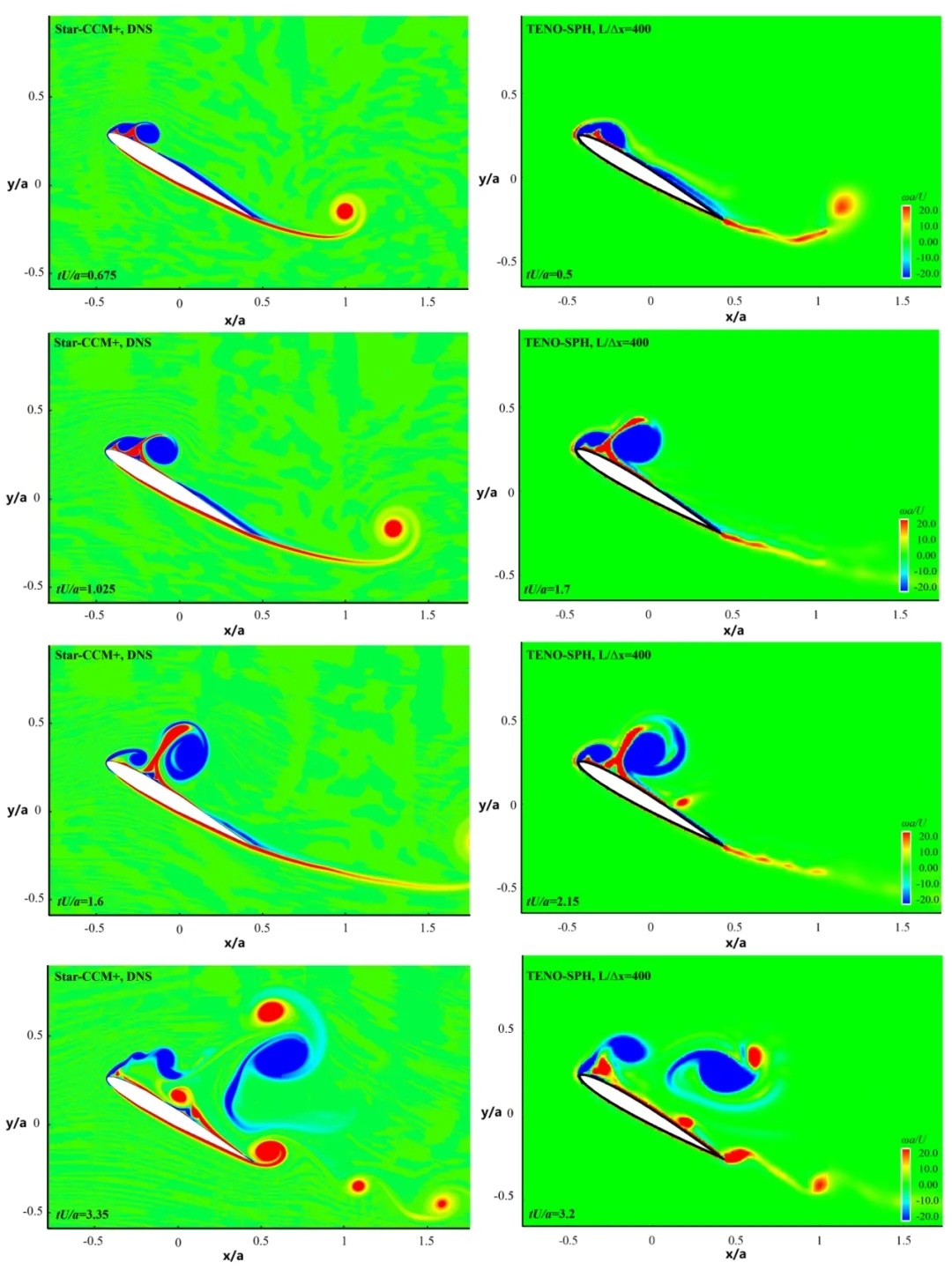
      该研究成果发表在计算力学权威期刊Computer Methods in Applied Mechanics and Engineering（中科院大类一区Top），第一作者为海洋工程与技术学院孟子飞博士后，通讯作者为孙鹏楠副教授。研究工作得到国家重点研发计划、国家自然科学基金、中国博士后面上基金、广东省杰出青年科学基金等项目支持，“海路通”超算集群提供了重要算力支撑。

编辑:范凌婧
一读:许璐洁
初审:曹雁群
复审:翟爱梅
审核发布:漆小萍